CUADRILATEROS

CUADRILATEROS:

La forma más habitual de clasificar cuadriláteros es por el paralelismo de sus lados. Según este criterio los  cuadriláteros pueden ser:

Las relaciones entre los lados y los ángulos de un cuadrilátero nos sirven para clasificarlos. A los cuadriláteros que tienen los lados paralelos dos a dos se les llama paralelogramos. Son paralelogramos, por tanto, el cuadrado, elrectángulo, el rombo y el romboide:

Características generales.

Un cuadrilátero es una figura plana formada por cuatro lados que se cortan dos a dos. Según la disposición de los lados y los ángulos que forman, se obtienen distintos tipos de cuadriláteros.

Cuando los lados son paralelos dos a dos, los cuadriláteros se llamanParalelogramos.

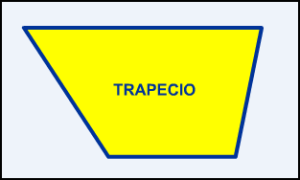
Cuando solamente son dos los lados paralelos, el cuadrilátero se llamaTrapecio.

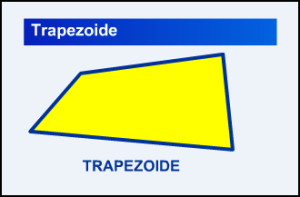
Cuando no existe ningún lado paralelo a otro, el cuadrilátero se llamaTrapezoide.

Diagonal: es la recta que une un vértice con otro no inmediato.

Tipos de cuadriláteros

1. PARALELOGRAMAMO. Un paralelogramo es un cuadrilátero que tiene sus lados paralelos dos a dos.
2. TRAPECIO. Es un cuadrilátero que tiene dos lados paralelos y los otros dos no.
3. TRAPEZOIDE. Es un cuadrilátero que no tiene ninguno de sus lados paralelo a otro.

CLASES DE PARALELOGRAMOS.

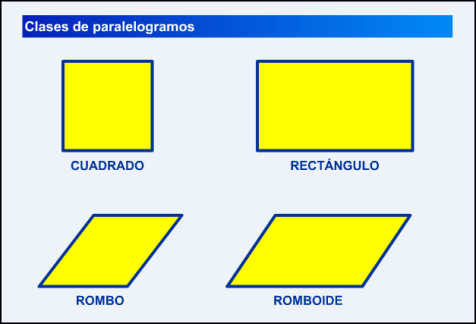
• El cuadrado tiene todos los lados iguales y sus vértices forman ángulos rectos (de 90º).
• El rectángulo tiene los lados iguales dos a dos. Sus vértices también forman ángulos rectos.
• El rombo tiene todos sus lados iguales pero sus vértices tienen ángulos distintos al ángulo recto e iguales dos a dos.
• El romboide tiene los lados iguales dos a dos y sus ángulos iguales dos a dos y distintos del ángulo recto.

CLASES DE TRAPECIOS.

• El trapecio tiene dos de sus cuatro lados paralelos, los otros dos no.
• El trapecio rectángulo se caracteriza porque uno de los ángulos es un ángulo recto.
• El trapecio isósceles se caracteriza porque sus dos lados no paralelos tienen el mismo tamaño.

3.2.1. Construir un cuadrado conociendo el lado.

OPERACIONES:

1. Se coloca el lado a (lado del cuadrado que se da como dato) en la posición de la base.
2. Desde los extremos del lado a, se trazan dos perpendiculares.
3. Mediante dos arcos, se lleva el lado a sobre las perpendiculares.
4. Se unen los cuatro puntos y se obtiene el cuadrado pedido.

3.2.2. Construir un cuadrado conociendo su diagonal d.

OPERACIONES:

1. Sobre un punto cualquiera se trazan dos rectas perpendiculares entre si: recta r y recta s.
2. Se traza la bisectriz del ángulo formado por las dos rectas r y s.
3. Sobre la bisectriz se lleva la diagonal.
4. Desde este punto se trazan paralelas a las rectas r y s.
5. Utilizando estos puntos, se construye el cuadrado.

3.2.3. Construir un rectángulo conocidos los lados.

OPERACIONES:

1. Sobre una recta cualquiera r se coloca un lado del rectángulo, por ejemplo el lado a.
2. Sobre un extremo del lado a (por ejemplo el punto A) se traza una recta sperpendicular a este lado y, sobre la perpendicular, se lleva el lado b.
3. Desde el otro extremo del lado a (punto B) se traza un arco de radio b.
4. Desde el punto D (extremo del lado b) se traza un arco de radio igual al lado a.
5. Se unen los cuatro puntos y se obtiene el rectángulo.

3.2.4. Construir un rectángulo conocidos la diagonal y un lado.

OPERACIONES:

1. Se coloca la diagonal d (segmento AB) sobre una recta cualquiera r.
2. Se halla el punto medio M de la diagonal y se traza una circunferencia que pase por sus extremos (puntos A y C).
3. Desde A y C se trazan dos arcos de radio a.
4. Se unen los puntos hallados (B y D), con los extremos de la diagonal (A y C), y se obtiene el rectángulo.

3.2.5. Construir un rombo conocidos una diagonal y su lado.

OPERACIONES:

1. Se coloca la diagonal sobre una recta r cualquiera. Se obtienen los puntos Ay C.
2. Con el lado a como radio, se trazan dos arcos desde A y C. Obtenemos los puntos B y D.
3. Se unen los extremos de la diagonal (A y C) con los puntos hallados (B y D) y se obtiene el rombo.

Mayor detalle

3.2.6. Construir un romboide conocidos los lados y la altura.

OPERACIONES:

1. Sobre una recta r cualquiera se coloca el lado AB.
2. Se traza una perpendicular al lado AB en uno de sus extremos (por ejemplo, en B) y se lleva la altura h.
3. Por el punto 1 se traza una paralela a lado AB. Desde los extremos A y B, se trazan dos arcos, de radio BC.
4. Se unen los puntos A, B, C y D y se obtiene el romboide.

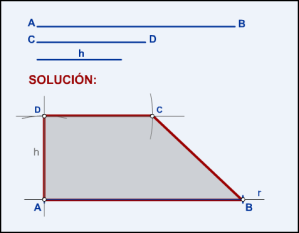
3.2.7. Construir un trapecio recto conocidos sus lados paralelos y la altura.

OPERACIONES:

1. Sobre una recta r cualquiera se coloca la base AB.
2. Se traza una perpendicular a AB en uno de sus extremos (por ejemplo en A) y se lleva la altura h.
3. Por D se traza una paralela a AB y se lleva la base superior CD.
4. Se unen los puntos A, B, C y D y se obtiene el trapecio recto.